卡尔曼滤波

阅读数: 次 2023-09-11

字数统计: 4.8k字 | 阅读时长: 18分

卡尔曼滤波与人体关节运动预测及平滑处理

这段时间在做一个项目，是有关于人体姿势识别的，我们采用的方案是多台Kinect v2设备捕捉关节点并记录处理，所以这里就必定就涉及到设备捕捉时的数据实时处理和再现时的数据预处理两个方面。虽然看起来好像没什么区别，但实际上还是非常不一样的。数据预处理相对来说简单一点（也是我最先实现的），因为只需要简单的将前后帧的数据结合处理就可以了，基本不需要考虑太多东西；但是实时处理就不太一样了，因为设备捕捉时不能获取到当前帧的后一帧，也不能延迟处理（先收集前后几帧的数据，再处理中间某一帧的数据），因为这样会引入较高的延迟，人体动作与捕捉到的区别会偏大，并不理想，且也不能使用过于复杂的算法，防止掉帧，丢失数据。

所以这样来看，思路其实就很清晰了，首先是捕捉时在帧率允许的前提下简单平滑一下各关节点的数据，从而消除部分抖动；其次在重现时考虑采用其他方法修改、消除与真实情况较大的数据（这时只需要考虑准确性就好了）。这里面比较难的地方可能就是关于实时处理这部分的方法，我当时第一反应就是使用大名鼎鼎的卡尔曼滤波来实现，用其前几帧的预测值作为当前帧，再做一个平滑处理。

当然，我还是按照我的步骤，介绍一下自己的实现方法。

数据记录

第一步肯定就是先记录Kinect的数据了。虽然理想情况是多台Kinect同时捕捉最后合并，但是现在还没做到这一步，就先以单台Kinect做一个示范。不过这个在网络上有很多代码示例。我这里参考的是这一版《使用Kinect_V2相机+pykinect2_识别并保存人体skeleton运动时序坐标信息》。代码如下所示：

import csv
import pygame
from pykinect2 import PyKinectRuntime, PyKinectV2
from pykinect2.PyKinectV2 import *
 
# 初始化Pygame
pygame.init()
 
# 设置窗口尺寸
width, height = 960, 540
size = (width, height)
screen = pygame.display.set_mode(size)
pygame.display.set_caption("PyKinect2 Body Tracking")
 
# 创建Kinect实例
kinect = PyKinectRuntime.PyKinectRuntime(PyKinectV2.FrameSourceTypes_Body)
 
# 创建CSV文件
with open('skeleton_data.csv', 'w', newline='') as csvfile:
    writer = csv.writer(csvfile)
    joint_ids = [joint_id for joint_id in range(0, PyKinectV2.JointType_Count)]
    header = ['Frame'] + [f'Joint {joint_id+1} X' for joint_id in joint_ids] + [f'Joint {joint_id+1} Y' for joint_id in joint_ids] + [f'Joint {joint_id+1} Z' for joint_id in joint_ids]
    writer.writerow(header)  # 写入表头
 
    # 游戏主循环
    running = True
    frame_count = 0
    frame_rate = 30  # 帧率设定为30帧/秒
    interval = 1.0 / frame_rate  # 计算每帧的时间间隔
    last_time = pygame.time.get_ticks() / 1000.0  # 上一帧的时间戳
    tracked_body_index = None  # 跟踪的人体索引
 
    while running:
        # 处理事件
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                running = False
 
        # 获取骨架数据
        if kinect.has_new_body_frame():
            bodies = kinect.get_last_body_frame().bodies
 
            if bodies is not None:
                # 寻找正在跟踪的人体
                for i in range(0, kinect.max_body_count):
                    body = bodies[i]
                    if body.is_tracked:
                        tracked_body_index = i
                        break
 
        # 跟踪到人体后才进行数据记录
        if tracked_body_index is not None:
            # 计算当前时间戳
            current_time = pygame.time.get_ticks() / 1000.0
 
            # 根据时间间隔记录数据
            if current_time - last_time >= interval:
                body = bodies[tracked_body_index]
                frame_data = []
 
                # 存储关节坐标数据
                for joint_id in range(0, PyKinectV2.JointType_Count):
                    joint = body.joints[joint_id]
                    frame_data.extend([joint.Position.x, joint.Position.y, joint.Position.z])
 
                # 调整关节坐标数据的排列顺序
                rearranged_data = []
                for joint_id in range(1, PyKinectV2.JointType_Count+1):
                    rearranged_data.extend(frame_data[(joint_id-1)*3 : joint_id*3])
 
                # 写入CSV文件
                writer.writerow([frame_count+1] + rearranged_data)
 
                # 打印关节数据
                print(f"Frame: {frame_count+1}, Joint Positions: {rearranged_data}")
 
                # 更新上一帧的时间戳
                last_time = current_time
 
                # 帧数加1
                frame_count += 1
 
        # 清空屏幕
        screen.fill((0, 0, 0))
 
        # 绘制骨架连线图
        if tracked_body_index is not None:
            joints = bodies[tracked_body_index].joints
 
            # 定义骨架连线关系
            bone_connections = [
                (JointType_Head, JointType_Neck),
                (JointType_Neck, JointType_SpineShoulder),
                (JointType_SpineShoulder, JointType_SpineMid),
                (JointType_SpineMid, JointType_SpineBase),
                (JointType_SpineShoulder, JointType_ShoulderRight),
                (JointType_SpineShoulder, JointType_ShoulderLeft),
                (JointType_ShoulderRight, JointType_ElbowRight),
                (JointType_ElbowRight, JointType_WristRight),
                (JointType_WristRight, JointType_HandRight),
                (JointType_ShoulderLeft, JointType_ElbowLeft),
                (JointType_ElbowLeft, JointType_WristLeft),
                (JointType_WristLeft, JointType_HandLeft),
                (JointType_SpineBase, JointType_HipRight),
                (JointType_SpineBase, JointType_HipLeft),
                (JointType_HipRight, JointType_KneeRight),
                (JointType_KneeRight, JointType_AnkleRight),
                (JointType_AnkleRight, JointType_FootRight),
                (JointType_HipLeft, JointType_KneeLeft),
                (JointType_KneeLeft, JointType_AnkleLeft),
                (JointType_AnkleLeft, JointType_FootLeft)
            ]
 
            # 绘制骨架连线
            for connection in bone_connections:
                joint1 = joints[connection[0]]
                joint2 = joints[connection[1]]
                if joint1.TrackingState == TrackingState_Tracked and joint2.TrackingState == TrackingState_Tracked:
                    joint1_pos = kinect.body_joint_to_color_space(joint1)
                    joint2_pos = kinect.body_joint_to_color_space(joint2)
                    pygame.draw.line(screen, (255, 0, 0), (joint1_pos.x, joint1_pos.y), (joint2_pos.x, joint2_pos.y), 5)
 
        # 更新屏幕显示
        pygame.display.flip()
 
    # 退出Pygame
    pygame.quit()
 
# 释放Kinect资源
kinect.close()

Tips：这里数据存储有一个小问题，就是在csv文件中第一行为数据标签Frame,Joint 1 X,Joint 2 X,Joint 3 X,Joint 4 X,Joint 5 X,Joint 6 X,Joint 7 X,Joint 8 X,Joint 9 X……看上去应该是将每个关节的坐标值依照X，Y，Z的顺序分别记录。但是实际上他的顺序是错的，实际上应该是Frame,Joint 1 X,Joint 1 Y,Joint 1 Z,Joint 2 X,Joint 2 Y,Joint 2 Z,Joint 3 X,Joint 3 Y,Joint 3 Z……也就是依据关节的顺序分别记录坐标值。

再依据写入代码和存储数据，简单写个程序，利用pygame重现二维数据。

2023-09-11 12-13-27 00_00_03-00_00_15

可以看出，如果就用直接记录的数据，基本上关节点大都每帧都在抖动，而且在多个关节点位置重叠时会更严重，也有一些大幅度动作会出现明显不正确的偏差。

数据预处理

首先还是从相对好上手的数据预处理开始。我这里说的预处理仅仅是一部分，只涉及到表面的处理，而不是关于神经网络处理或者正向运动学、反向运动学等其他方面的知识（这也是我们后面可能要处理的问题，如果能做到那里到时候应该还会简单聊一聊）。

根据我大致地调研和尝试后，选择了一个相对好实现也很好理解的方法。简单来说就是抽取某一段帧中的数据，将其处理后的数据作为其中间的帧的数据，依次类推，从而实现对每一帧数据的处理。

那具体应该怎么实现呢？我的思路就是去除极值、再取其均值。我自己尝试使用了几种可行的方法，比如单纯使用均值处理，但是在我记录的数据中有一些关节点的偏差明显较大，只是均值处理只能将数据平滑显示，但是具体显示就好像是单纯延迟一样，除了画面稳定了一些之外并没有什么剔除误差，这不太符合我的设想。所以我就考虑两个方向：略微扩大帧的范围以及去除极值。经过测试，我发现单纯使用前一种方法虽然使误差显得没有那么大了，但是其延迟也更加明显，关节的运动轨迹也变得不太符合人体运动，平滑过头了。而后一种情况，我先是尝试采用网上的MAD法、3σ法、百分法这类方法，但在实验中发现，其帧率会明显下降至10帧左右甚至都不到，虽然处理效果好了一些，但目前来说仅仅一个预处理就这么耗费性能，我是不太满意的。

简单看一眼代码就知道，这些方法基本都是通过确认其数据在整体中的位置，计算其是否超出给定的比值范围。很明显，这样的方法更适合用在横向数据量大的情况，而不适用于我这种情况。所以没必要照着网上的抄，简单改造一下就可以了。

1
2
3

def dataSort(data,n=2):
    np.sort(data)
    return data[n:len(data)-n]

返回的结果是一个去除了两个极大值和两个极小值的列表，只需要加一个np.mean()求个平均值就ok了，可以说是非常地简单易懂（

我这里运行的结果是这样的：

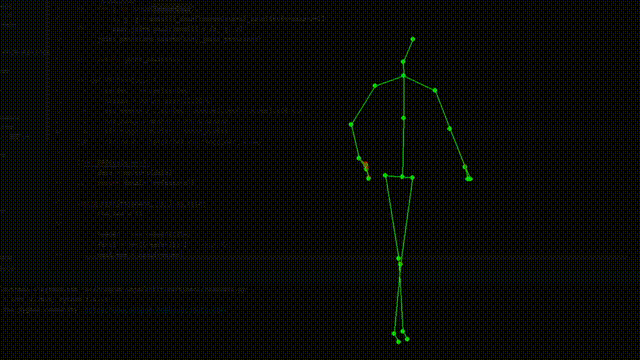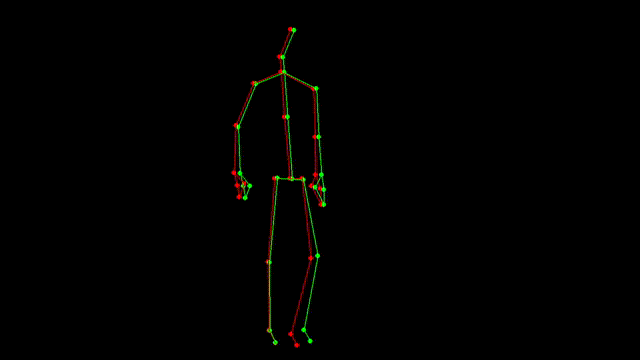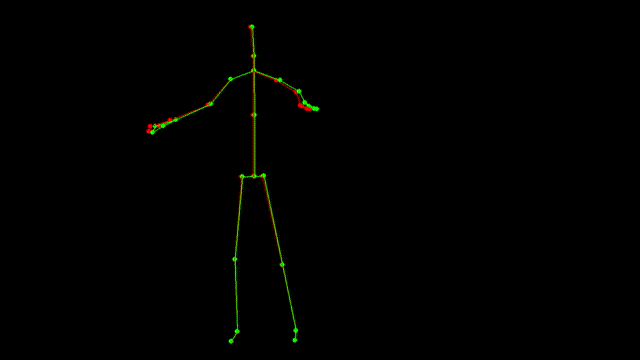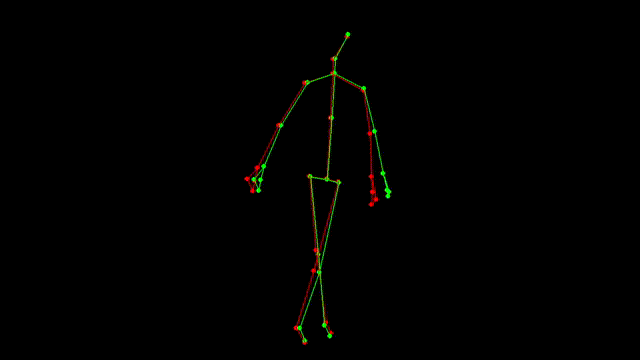
2023-09-11 10-33-17 00_00_03-00_00_14

红色为当前帧的关节数据，绿色为处理过后的关节数据

看起来好了很多，抖动和个别偏差情况都改善了不少。

这里我用了前后共11帧的数据处理才能实现这种效果，帧数据过少部分偏差值仍然较大，帧数据过多则会导致过度平滑。我是取中间帧的数据作为红色的当前帧的真实数据展示的，这也是为什么不能实时处理的原因：5帧的差距会带来0.1s的误差，虽然看起来不大，但是反应在视频里就会看到关节（特别是末端）延迟会非常巨大。

数据实时处理

现在就要来到相对来说有一点点困难的地方：实时处理。那么就像前面说的一样，我们先从卡尔曼滤波入手，简单介绍一下其原理。我参考的主要是《图说卡尔曼滤波，一份通俗易懂的教程》。这篇文章里有许多可视化的图像说明，相对更好理解一点。我这里主要是整理并说明了一些刚开始阅读时没太理解的内容。（我自己最开始是连图都没看懂的hhh所以才想写篇总结一下）。

当然，如果你不想看原理，只是想看看代码，可以参考一下这篇文章《目标估计模型-卡尔曼滤波》写得非常好，代码解释非常详细，我也是在看完代码解释后才逐渐理解整体过程的。也可以点这里看我实现的效果。

卡尔曼滤波

只要是存在不确定信息的动态系统，卡尔曼滤波就可以对系统下一步要做什么做出有根据的推测。即便有噪声信息干扰，卡尔曼滤波通常也能很好的弄清楚究竟发生了什么，找出现象间不易察觉的相关性。

这是很多博客对卡尔曼滤波的说明，简单来说就是，卡尔曼滤波可以从前几帧的结果出发，用输入状态生成预测的输出状态，这一过程中可以避免部分外界因素的干扰，且可以计算出当前帧与之前的误差作为噪声，并传递给下一帧的预测中进行校正并更新。

不仅如此，卡尔曼滤波还有其他好处，比如内存占用小、速度快，之前常常在嵌入式开发中看见过他。因此，这个算法也非常契合我的需求，可以在视频流帧率基本不被干扰的前提下，对25个关节点的XYZ三维数据进行处理。

我们从物体运动开始做一个简单的推理：

现在存在一个在二维平面上到处移动的小车，那么其具有四个状态变量：坐标x，坐标y，x方向速度vx，y方向速度vy。其中，vx和vy是可以根据坐标计算出来的，也就是说，小车实际上只具有两个观测输入：坐标x，坐标y。

那么也就是说，小车每帧的移动是符合以下公式的。 \[ X_k=X_{k-1}+\Delta{X}=X_{k-1}+\Delta{t}*Vx_{k-1} \\ Y_k=Y_{k-1}+\Delta{Y}=Y_{k-1}+\Delta{t}*Vy_{k-1} \\ Vx_{k}=Vx_{k-1}\\ Vy_{k}=Vy_{k-1} \\ \] 也就是当前位置=上一帧位置+帧时间*上一帧速度

然后再把坐标和速度统一成矩阵\(p_{k}\)和\(v_{k}\)，原式就可以表示为： \[ p_k=\begin{bmatrix} X_k\\ Y_k \end{bmatrix}\quad v_k=\begin{bmatrix} Vx_k\\ Vy_k \end{bmatrix}\\ \] 然而，这样的一个运动系统是非常理想化的。在运动过程中，小车可能会因为动力的变化出现加速度变化，这是可以测量量化、计算的指标。如果只有这种变化，那么我们可能用GM（灰色预测模型）就能实现。而在更真实的情况下，小车会因为地面摩擦力、空气阻力甚至是地面上一个小石子都会对其运动造成或多或少的影响，这些都是无法测量甚至都不确定是否存在的指标。这就该轮到卡尔曼滤波上场了。

卡尔曼滤波假设两个变量（在例子中是位置和速度）都应该是随机的，而且符合高斯分布。每个变量都有一个均值 \(μ\) ，它是随机分布的中心；有一个方差 \(σ^2\) ，它衡量组合的不确定性。因此，我们需要知道两个有关k的信息：最佳估计 \(x_{k}\) （均值，也就是 μ ），协方差矩阵 \(P_{k}\) 。 \[ f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \] 在概率论中我们知道，想知道事件的相关性时需要计算其协方差。在卡尔曼滤波中也是一样，为了捕捉各个变量之间的关系，我们需要建立一个协方差矩阵 \(P_{k}\) ，并将其作为方差 \(σ^2\) 。我们用 \(Σ\) 表示协方差矩阵，在这个例子中，就是 \(Σ_{ij}\) 。这样就可以得到： \[ P_{k}=\begin{bmatrix} \sum_{pp} \quad \sum_{pv}\\ \sum_{pv} \quad \sum_{vv} \end{bmatrix} \] 我们先处理一下表示最佳估计的均值 \(x_{k}\) ： \[ \begin{align*} x_k &= \begin{bmatrix} p_k\\ v_k \end{bmatrix}\\ &= \begin{bmatrix} 1 \ \Delta{t}\\ 0 \quad 1 \end{bmatrix}x_{k-1}\\ &=F_{k}x_{k-1} \end{align*} \] 现在我们就得到了一个表示预测矩阵\(x_{k}\)。但我们还不知道协方差矩阵是怎么更新的，所以我们先推导一下，将 \(Cov(x)\) 协方差矩阵分布中的每个点乘以矩阵A，得到： \[ Cov(x)=Σ\\ Cov(Ax)=AΣ A^{T} \] 由此，我们就可以推导出用于先验估计的协方差矩阵。 \[ \begin{align*} P_{k }&= Cov(x_k)\\ &= Cov(F_k x_{k-1})\\ &= F_{k}P_{k-1}F_{k}^{T} \end{align*} \]

外部不确定性

前面我们说到，在真实情况中，有很多无法测量的外部因素影响。为了处理这种影响，我们需要在预测步骤后加入一个新的不确定性，用于模拟所有外界环境中相关的不确定性。而这种不确定性可以视为协方差矩阵 \(Q_k\) 的噪声。所以，我们再对 \(P_k\) 处理一下，得到： \[ P_k=F_k P_{k-1} F_k^T + Q_k \] 我看到有一个特别好的解释就是：新的不确定性 \(P_k\) 是基于原不确定性原不确定性 \(P_{k-1}\) 和外部环境的不确定性 \(Q_k\) 得到的预测。

细化估计值

我们可能有好几个传感器，它们一起提供有关系统状态的信息。传感器的作用不是我们关心的重点，它可以读取位置，可以读取速度，重点是，它能告诉我们关于状态的间接信息——它是状态下产生的一组读数。

所以，我们需要将传感器读取的数据单独处理，这就需要传感器读数矩阵 \(H_k\) 。这个矩阵乘以 \(x_k\) 后得到的就只有观测输入的数据。在本例子中，原 \(x_k=\begin{bmatrix} p_k \\ v_k \end{bmatrix}\) ，处理后得到： \[ \begin{align} x_k'&=H_k x_k\\ &=\begin{bmatrix} 1 \quad 0 \end{bmatrix} \begin{bmatrix} p_k \\ v_k \end{bmatrix}\\ &=\begin{bmatrix} 1 \quad 0 \quad 0 \quad 0 \\ 0 \quad 1 \quad 0 \quad 0 \\ \end{bmatrix} \begin{bmatrix} X_k\\ Y_k\\ Vx_k\\ Vy_k \end{bmatrix}\\ &=\begin{bmatrix} X_k\\ Y_k\\ \end{bmatrix}\\ &=\begin{bmatrix} p_k \end{bmatrix}\\ \end{align} \] 也就可以得到： \[ \mu_{expected} = H_k x_k\\ Σ_{expected} = H_k P_k H_x^T \] 我们将这种由传感器带来的不确定性（也就是噪声）的协方差称为 \(R_k\) ，读数的平均值记为 \(z_k\) 。

现在我们得到了两块高斯分布，一块围绕预测的均值，另一块围绕传感器读数。我们可以通过两块高斯分布相乘的方法，得到它们的重叠部分，这也是会出现最佳估计的区域，也就是一个拥有独立均值和协方差矩阵的新高斯分布。过程我就不详细证明了，其结论就是： \[ \begin{align} \mu&=\mu_1 + \frac{\sigma_1(\mu_2-\mu1)}{\sigma_1^2 + \sigma_2^2}\\ \sigma^2 &= \sigma_1^2 - \frac{\sigma_1^4}{\sigma_1^2 + \sigma_2^2} \end{align} \] 令 \(k=\frac{\sigma_1^2}{\sigma_1^2 + \sigma_2^2}\) ，得： \[ \begin{align} \mu&=\mu_1 + k(\mu_2-\mu1)\\ \sigma^2 &= \sigma_1^2 - k\sigma_1^2 \end{align} \] 转化为高维的矩阵为： \[ \begin{align} K&=\frac{Σ_1}{Σ_1+Σ_2} \\ \mu'&=\mu_1' + K(\mu_2'-\mu_1')\\ \sigma'^2 &= Σ_1^2 - KΣ_1^2 \end{align} \] 而这个矩阵K就是我们说的卡尔曼增益。

所以现在，我们需要的东西都齐了。一个是矩阵计算得到的预测值 \((H_kx_k, H_k P_k H_k^T)\) 形成的高斯分布，另一个则是通过传感器读出的真实值 \((z_k, R_k)\) 形成的高斯分布。即可以得到： \[ \begin{align*} \mu_1 &= H_kx_k & \Sigma_1 &= H_k P_k H_k^T\\ \mu_2 &= z_k & \Sigma_2 &= R_k\\ \end{align*} \] 代回原方程中得到： \[ \begin{align*} x_k'&=x_k+K'(z_k-H_kx_k)\\ P_k' &= P_k-K'H_kP_k\\ K' &= \frac{P_kH_k}{H_kP_kH_k^T+R_k} \end{align*} \] 而这个 \(x_k'\) 就是我们想算出的最佳估计值，它也可以作为下一帧的 \(x_k\) 继续预测（也就是 \(x_k'=x_{k-1}'++K'(z_k-H_kx_{k-1}')\)）

卡尔曼滤波的原理和推导就到这里了！是不是非常的轻松呢~

实现效果

如果你看懂了上面的过程，直接看那篇文章《目标估计模型-卡尔曼滤波》就可以了，里面代码中所需的参数和文章里的提到的参数完全一致，只需要根据需求改一下就好了。

这里展示一下我的效果图：

2023-09-11 22-11-37 00_00_03-00_00_14

好像，好了一点，但没完全好。抖动还是很厉害啊，可能是因为原数据实在是太惨不忍睹了吧（

那该咋办呢？我尝试的方案就是仿照之前数据预处理的方法，抽出前几帧的数据，求一个平均值再作为update()中的三维数据进行更新。我也尝试了在前几帧范围内去除1-2个极大、极小值后再平均，或者以剩余数据中较大的一组作为上一帧数据更新的方法，但是效果似乎都不太好。目前方案的效果如下：

2023-09-11 22-10-37 00_00_03-00_00_14

可以看出来，关节移动相对更平滑了一些，肢体末端的关节也不会出现剧烈抖动，不过腿在移动的时候误差似乎增大了一些，感觉也还在可接受范围内。

当然，除了卡尔曼滤波之外，还有其他不少方法实现数据平滑处理的。比如说移动平均法、指数平滑法、中值滤波、ARMA模型(auto regressive moving average model)自回归滑动平均模型、Savitzky-Golay 滤波器等等等等，后面如果有机会深入了解的话我再来做些简单的介绍。